#include <ClassicalPolynomial.hpp>
|
| | ClassicalPolynomial () |
| |
| | ClassicalPolynomial (const 1 &) |
| |
| virtual | ~ClassicalPolynomial () |
| |
| double | eval (double x) const override |
| | ICloneable interface.
|
| |
| void | evalOpTraining (MatrixSparse *Op, const constvect inv, 1 &store, 1 &work) const override |
| |
| void | evalOpCumul (MatrixSparse *Op, const constvect inv, vect outv) const |
| |
| void | evalOp (MatrixSparse *Op, const constvect inv, vect outv) const override |
| |
| double | evalOpByRank (MatrixSparse *S, Id rank) const override |
| | Returns the rank-th term of the Diagonal of 'Op' in its Polynomail expression through Horner mechanism It is similar to the method 'evalOp' but targets the diagonal only.
|
| |
| void | _addEvalOp (const ALinearOp *Op, const constvect inv, vect outv) const override |
| |
| | APolynomial () |
| |
| | APolynomial (const 1 &coeffs) |
| |
| | APolynomial (const APolynomial &m) |
| |
| APolynomial & | operator= (const APolynomial &p) |
| |
| virtual | ~APolynomial () |
| |
| String | toString (const AStringFormat *strfmt=nullptr) const override |
| | Interface for AStringable.
|
| |
| void | init (const 1 &coeffs) |
| |
| | evalOp (MatrixSparse *Op, const constvect inv) const |
| |
| void | addEvalOp (const ALinearOp *Op, const constvect inv, vect outv) const |
| |
| | getCoeffs () const |
| |
| void | setCoeffs (const 1 &coeffs) |
| |
| Id | getDegree () const |
| |
| virtual Id | fit (const std::function< double(double)> &f, double from=0., double to=1., double tol=EPSILON5) |
| |
| | AStringable () |
| |
| | AStringable (const AStringable &r) |
| |
| AStringable & | operator= (const AStringable &r) |
| |
| virtual | ~AStringable () |
| |
| virtual void | display (const AStringFormat *strfmt=nullptr) const final |
| |
| virtual void | display (Id level) const final |
| |
| | ICloneable () |
| |
| virtual | ~ICloneable () |
| |
| virtual ICloneable * | clone () const =0 |
| |
| std::shared_ptr< ICloneable > | cloneShared () const |
| |
| std::unique_ptr< ICloneable > | cloneUnique () const |
| |
◆ ClassicalPolynomial() [1/2]
| gstlrn::ClassicalPolynomial::ClassicalPolynomial |
( |
| ) |
|
◆ ClassicalPolynomial() [2/2]
| gstlrn::ClassicalPolynomial::ClassicalPolynomial |
( |
const 1 & |
coeffs | ) |
|
◆ ~ClassicalPolynomial()
| gstlrn::ClassicalPolynomial::~ClassicalPolynomial |
( |
| ) |
|
|
virtual |
◆ _addEvalOp()
◆ eval()
| double gstlrn::ClassicalPolynomial::eval |
( |
double |
x | ) |
const |
|
overridevirtual |
◆ evalOp()
◆ evalOpByRank()
| double gstlrn::ClassicalPolynomial::evalOpByRank |
( |
MatrixSparse * |
S, |
|
|
Id |
rank |
|
) |
| const |
|
overridevirtual |
Returns the rank-th term of the Diagonal of 'Op' in its Polynomail expression through Horner mechanism It is similar to the method 'evalOp' but targets the diagonal only.
- Parameters
-
| S | Target Sparse matrix (possibly not even concretized) |
| rank | Rank of the target |
- Returns
- double
Reimplemented from gstlrn::APolynomial.
◆ evalOpCumul()
◆ evalOpTraining()
| void gstlrn::ClassicalPolynomial::evalOpTraining |
( |
MatrixSparse * |
Op, |
|
|
const constvect |
inv, |
|
|
1 & |
store, |
|
|
1 & |
work |
|
) |
| const |
|
overridevirtual |
The documentation for this class was generated from the following files:
- include/Polynomials/ClassicalPolynomial.hpp
- src/Polynomials/ClassicalPolynomial.cpp
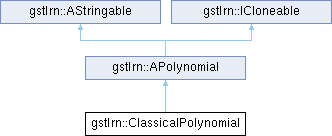
 Public Member Functions inherited from gstlrn::APolynomial
Public Member Functions inherited from gstlrn::APolynomial Public Member Functions inherited from gstlrn::AStringable
Public Member Functions inherited from gstlrn::AStringable Public Member Functions inherited from gstlrn::ICloneable
Public Member Functions inherited from gstlrn::ICloneable